Bạn có chắc chắn muốn xóa bài viết này không ?
Bạn có chắc chắn muốn xóa bình luận này không ?
ECDSA là viết tắt của Elliptic Curve Digital Signature Algorithm, tạm gọi là thuật toán chữ kí số đường cong Elliptic. Đây là 1 thuật toán nổi tiếng trong mật mã học, thường được sử dụng trong các nền tảng blockchain, ví dụ như Bitcoin, Ethereum ...
Thuật toán này được sử dụng để tạo chữ kí số (digital signature) cho dữ liệu (ví dụ 1 tệp tin) giúp ta có thể xác minh tính xác thực của dữ liệu mà không ảnh hưởng đến độ bảo mật của nó. Có thể so sánh chữ kí số với chữ kí ngoài đời thực về tác dụng của nó, có 1 chút khác biệt là ngoài đời ta có thể giả mạo chữ kí của người khác mà không bị phát hiện nhưng ECDSA signature thì ta không thể giả mạo.
Nguyên lí của thuật toán rất đơn giản, ta có 1 phương trình toán học được thể hiện bằng 1 đường cong Elliptic trên đồ thị.
Chọn 1 điểm bất kì nằm trên đường cong trên đồ thị và coi đó là điểm gốc (Điểm G) - Điểm này thường là 1 điểm cố định trong 1 triển khai nhất định. Ví dụ, tất cả các cặp khóa trong bitcoin đều có chung 1 điểm G.
Chọn 1 số ngẫu nhiên, đây chính là private key.
Ta sử dụng 1 phương trình toán học nào đó, tạm gọi là magical mathematical equation sử dụng số ngẫu nhiên và điểm gốc ở trên để tìm ra 1 điểm khác trên đường cong, điểm này chính là public key.
Khi ta muốn kí 1 file, ta sử dụng private key cùng với hàm băm của file này làm đầu vào cho 1 phương trình toán học và sẽ tạo ra digital signature (chữ kí số). Chữ kí được chia thành 2 phần R và S. Để xác minh chữ kí là chính xác, ta chỉ cần public key làm đầu vào cho 1 phương trình toán học khác cùng với phần S của chữ kí, nếu nó được kí chính xác bởi private key, nó sẽ cho ra R. Túm váy lại, một chữ kí bao gồm 2 số R và S, ta sử dụng private key để tạo ra R và S và nếu 1 phương trình toán học sử dụng public key và S cung cấp cho ta số R thì chữ kí đó là hợp lệ. Không có cách nào để biết private key hoặc tạo chữ kí với public key
Phần này có thể hơi hại não với 1 số anh em nên mình sẽ cố gắng trình bày 1 cách dễ hiểu nhất :D.
ECDSA chỉ sử dụng toán học số nguyên, phạm vi của các số bị ràng buộc bởi số lượng bit được sử dụng trong chữ kí, thông thường ECDSA sẽ sử dụng tổng cộng 160 bit do đó sẽ có 1 phạm vi tương đối rộng đủ được coi là an toàn (phải tốn 1 lượng tính toán không tưởng để tấn công vét cạn và không khả thi với năng lực phần cứng hiện tại).
ECDSA sử dụng hàm băm mật mã SHA1 để băm thông điệp và kí vào thông điệp đã được băm. Hàm băm đơn giản là 1 phương trình toán học mà với mỗi thay đổi dù là nhỏ nhất ở đầu vào, nó sẽ cho ra đầu ra hoàn toàn khác, SHA1 luôn cho ra đầu ra với kích thước cố định là 160 bit (tương đương 20 byte), điều này đặc biệt hữu ích với ECDSA để tăng tính bảo mật của giải thuật.
Bây giờ chúng ta sẽ xem nó hoạt động như thế nào, đường cong Elliptic dựa trên 1 phương trình toán học có dạng:
y^2 mod p = (x^3 + a * x + b) mod p
Nhìn vào phương trình ta có thể thấy phạm vi của y^2 sẽ nằm từ 0 đến p -1, cho chúng ta tổng số p giá trị có thể, tuy nhiên do ECDSA chỉ xử lí với số nguyên nên trong khoảng từ 0 đến p -1 chỉ có tập hợp nhở hơn các số là số chính phương (bình phương của 1 số nguyên). Vì vậy, đường cong này sẽ chưa 1 số điểm hữu hạn trên nó và ta có thể thấy mỗi điểm x sẽ cho ra 2 giá trị của điểm y => đường cong đối xứng qua trục X.
Một phép toán quan trọng trong ECDSA là phép cộng. Phép cộng được định nghĩa như sau:
Cho 2 điểm P và Q nằm trên đường cong elliptic, đường thằng đi qua 2 điểm P và Q cắt đường cong tại 1 điểm R, lấy điểm đối xứng với R qua trục X, điểm này chính là kết quả của P+Q. Hình minh họa:
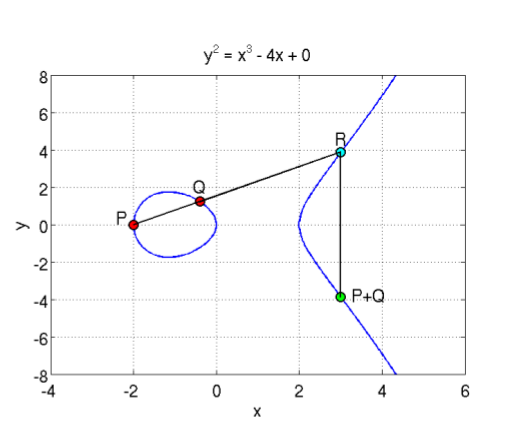
Với phép cộng với chính nó, ví dụ P + P, ta kẻ 1 đường thằng tiếp tuyến với đường cong, cắt đường cong tại 1 điểm, lấy điểm đối xứng của điểm đó qua trục X ta được điểm P + P. Do đó ta có thể dễ dàng định nghĩa phép nhân điểm P với 1 số nguyên dương: 2P = P + P, 3P = P + P + P...
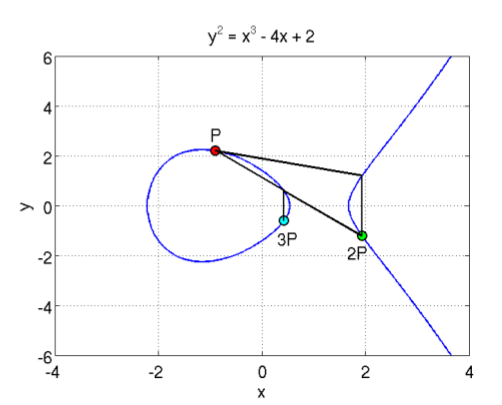
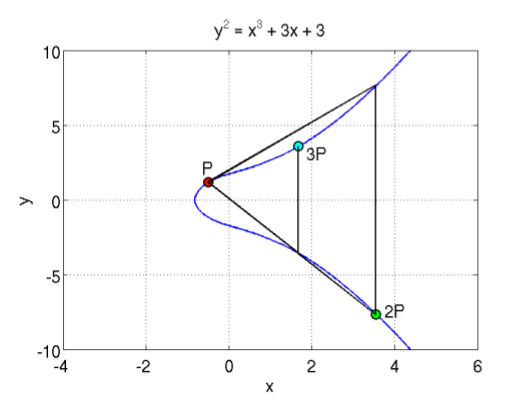
Còn tiếp ...
