Bạn có chắc chắn muốn xóa bài viết này không ?
Bạn có chắc chắn muốn xóa bình luận này không ?
Bug là một thuật ngữ mà khi nhắc đến thì mỗi lập trình viên đều muốn tránh xa. Nên người ta đã đưa ra các rất nhiều phương pháp để hạn chế nó. Trong đó, có cả các kỹ thuật kiểm thử phần mềm (testing) được rất nhiều người áp dụng.
Kỹ thuật kiểm thử phần mềm được phân ra làm 2 loại chính:
Theo Wikipedia - Black-box testing
"Black-box testing is a method of software testing that examines the functionality of an application without peering into its internal structures or workings"
Được tạm dịch là:
"Kiểm thử hộp đen là một phương pháp kiểm thử chức năng mà không cần bất kỳ kiến thức về cấu trúc và hành vi bên trong phần mềm."
Theo Wikipedia - White-box testing
"White-box testing is a method of testing software that tests internal structures or workings of an application, as opposed to its functionality"
Được tạm dịch là:
"Kiểm thử hộp trắng là một phương pháp kiểm thử được cấu trúc nội bộ hoặc hoạt động của một chương trình, như tương phản với chức năng được bộc lộ của người dùng cuối."
Thông thường, sau khi code xong một vài chức năng thì chúng ta thường sử dụng các công cụ như junit testing để kiểm thử cho ứng dụng.
Vậy làm thế nào để biết được số testcase mà mình đưa ra đã đầy đủ chưa?.
Trong kiểm thử hộp trắng, có rất nhiều phương pháp được đưa ra. Trong bài này mình xin trình bày một trong các phương pháp rất phổ biến của nó - Kiểm thử đường dẫn cơ sở
Kiểm thử đường dẫn cơ sở là phương pháp Kiểm thử bao quát các dòng source code, nhánh và đường dẫn. Phương pháp này giúp thu được các testcase từ đường cơ sở, được xác định theo biểu đồ dòng chảy của chương trình.
Các bước thực hiện:
- Xây dựng một đồ thị dòng chảy dựa trên logic của chương trình.
- Tính toán độ phức tạp Cyclomatic của đồ thì dòng chảy.
- Xác định đường cơ sở.
- Kiểm tra nếu số đường cơ sở không nhiều hơn độ phức tạp Cyclomatic.
- Thiết kế trường hợp thử nghiệm để kiểm tra các đường cơ sở .
Đồ thị dòng là một kỹ thuật dựa trên cấu trúc điều khiển của chương trình. Nó khá giống đồ thị luồng điều khiển của chương trình.
Chúng ta xây dựng đồ thị luông điều khiển của trương trình từ việc phân tích source code.
Ví dụ: Đồ thị luông điều khiển của trương trình có dạng như hình dưới.
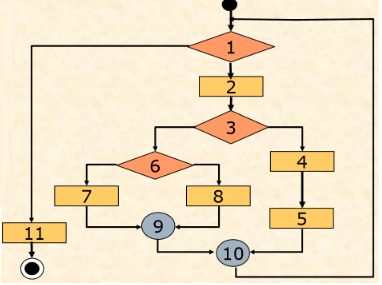
Từ đồ thị luồng điều khiển, chúng ta thu được đồ thị dòng bằng cách:
- Gộp các lệnh tuần tự , có nghĩa là gộp các nút mà từ nút này luôn đi qua nút kia.
- Thay lệnh rẽ nhánh và điểm kết thúc của các đường điều khiển bằng 1 nút vị tự
Ví dụ chúng ta xét luôn ví dụ từ đồ thị luồng ở trên:
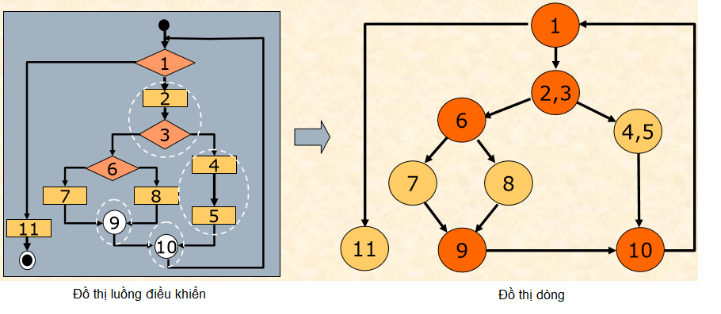
Ở ví dụ trên, ta thấy nút 2 và 3 có thể ghép được với nhau vì dòng chảy từ 2 luôn luôn đi qua 3, tương tự cho nút 4 và 5, và cũng tương tự cho nút 9 và 10
Sau khi biến đổi từ đồ thị luồng điều khiển, đồ thị dòng có cấu trúc:
- Mỗi nút (hình tròn) biểu thị một hay một số lệnh tuần tự, hoặc thay cho điểm hội tụ các đường điều khiển.
- Mỗi cạnh nối hai nút biểu diễn dòng điều khiển
Từ đó ta thu được các thông số như sau:
- 9 nút (trongđó 5 nút là vị tự (mầuđỏ) - Xin nhắc lại: nút vị tự là nút rẽ nhánh hoặc nút kết thúc rẽ nhánh)
- 11 cung
- Chia mặt phẳng thành 4 miền (Số miền được xác định như hình trên, phần đánh số màu xanh lá cây)
Từ các thông số ở trên, chúng ta tính toán độ phức tạp của đồ thị, việc tính này cho phép mình biết được chính xác có bao nhiêu đường dẫn cơ sở.
Độ phức tạp (ký hiệu V(G) ) được tính theo một trong các công thức sau:
- V(G) = E - N + 2 (= 11-9+2 = 4)
- V(G) = số miền phẳng (= 4)
- V(G) = P – 1 (= 5-1 =4)
Trong đó: E=số cung; N=số nút; P=số nút vị từ
Với ví dụ về đồ thị dòng ở trên ta có: V(G) = 4
Dựa vào độ phức tạp ở trên, chúng ta đã biết được có bao nhiêu đường dẫn cơ sở mà không sợ bị bỏ sót (Số đường cơ sở chính là độ phức tạp đồ thị)
Bây giờ chúng ta đi xác định đường cơ sở:
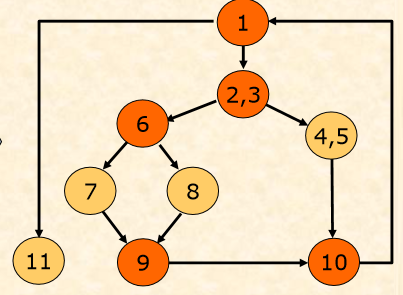
Từ đồ thị dòng, chúng ta đưa ra các đường cơ sở sau:
- 1 > 11
- 1 > 2,3 > 6 > 7 > 9 > 10 > 1
- 1 > 2,3 > 6 > 8 > 9 > 10 > 1
- 1 > 2,3 > 4,5 > 10 > 1
Chúng ta kiểm tra lại số đường cơ sở đã bằng với độ phức tạp chưa, nếu ít hơn thì chứng tỏ chúng ta đã đưa ra thiếu, nếu nhiều hơn thì một số đường cơ sở chúng ta đưa ra bị thừa hoặc bị trùng lặp với các đường cơ sở còn lại
Dựa vào đường cơ sở, chúng ta đưa ra các điều kiện sao cho thõa mãn các điều kiện để chúng đi hết các đường cơ sở đấy => và nó được xem như là 1 testcase
Cấu trúc:
Test case cho đường dẫn 1
- Đầu vào: …
- Đầu ra mong muốn: …
- Mục đích: …
....
Lý thuyết vậy đủ rồi, chúng ta đi đến phần thực hành thôi!
Ví dụ: Cho đoạn trương trình sau:
public int binarySearch(int sortedArray[ ], int searchValue) {
int bottom = 0;
int top = sortedArray.length - 1;
int middle, locationOfsearchValue;
boolean found = flase;
locationOfsearchValue = -1; /* the location of searchValue in the sortedArray */
/* location = -1 means that searchValue is not found */
while ( bottom <= top && !found) {
middle = (top + bottom)/2;
if (searchValue == sortedArray[ middle ])
{
found = true;
locationOfsearchValue = middle;
}
else if (searchValue < sortedArray[ middle ])
top = middle - 1;
else bottom = middle + 1;
} // end while
return locationOfsearchValue;
}
Ta gom các đoạn mã lại cho đỡ rối và thu bé số nút lại (việc này không ảnh hưởng gì tới độ phức tạp vì việc thu gọn này là gom các đoạn code luôn chạy cùng với nhau thành 1 khối, giống như việc chúng ta gộp nút ở lúc biến đổi từ biểu đồ luồng điều khiển sang biểu đồ dòng, nhưng đây mình làm tắt và bỏ qua bước xây dựng biểu đồ luồng điều khiển nên chúng ta gộp code thay vì gộp nút)

Xác định đường cơ sở
Đưa ra testcase
